Vermögensentwicklung mit diskreter logistischer Gleichung

\[ \frac{\Delta {x_{ t } }}{\Delta {t} }=\frac{ _{ x_{t+1}-x_t } }{ t_{t+1}-t_t }=r*x_{ t }*(1-\frac{x_{ t }} {K}) \] \[ \begin{aligned} x_{t+1} &: \text{Vermoegen zum Zeitpunkt t+1} \\ x_{t} &: \text{Vermoegen zum Zeitpunkt t} \\ x_{0} &: \text{AnfangsVermoegen} \\ K &: \text{Kapazitätsgrenze (Sättigungsniveau)} \\ r &: \text{intrinsische Wachstumsrate} \\ t &: \text{aktuelles Jahr} \end{aligned} \]

Die Veränderung des Vermögens hängt von der Wachstumsrate ab und dem aktuellen Vermögen mit einer Grenze \[ (1-\frac{x_{ t }} {K}) \] , der das Wachstum beschränkt. Wenn die Grenze erreicht ist wird x/K = 1 und der Faktor 0. Umwandlung der Folge:

\[ \frac{ _{ x_{t+1}} }{ 1 }=x_t + r*(x_{ t }-\frac{x_{ t }^2}{K}) \] \[ x_{t+1} =x_t + r*x_{ t }-r*\frac{x_{ t }^2}{K} = (1+r)* x_{ t } -r*\frac{x_{ t }^2}{K} \]

(1+r) ist wie beimZins. Es gibt eine negative Rückkopplung r*x^2/K

Es gibt eine Schleife über n = 50 Jahre. Die ersten Jahre sind unten gezeigt: \[ t = 0 \] \[ X[0] = 1.000.000\text{€} \] \[ X[1] = (1+r)* X[0] - r*\frac{X[0]^2}{K} = (1+0,3)* 1.000.000 - 0,3*\frac{1.000.000^2}{1.000.000.000} = 1.299.700 \text{€} \] \[ t = 1 \] \[ X[2] = (1+r)* X[1] - r*\frac{X[1]^2}{K} = (1+0,3)* 1.299.700 - 0,3*\frac{1.299.700^2}{1.000.000.000} = 1.689.103\text{€} \] \[ t = 2 \] \[ X[3] = (1+r)* X[2] - r*\frac{X[2]^2}{K} = (1+0,3)* 1.689.103 - 0,3*\frac{1.689.103^2}{1.000.000.000} = 2.194.978 \text{€} \] \[ t = 3 \] \[ X[4] = (1+r)* X[3] - r*\frac{X[3]^2}{K} = (1+0,3)* 2.194.978 - 0,3*\frac{ 2.194.978^2}{1.000.000.000} = 2.852.026\text{€} \]

Die Berechnungen kann man mit einem Python Skript machen. Der Plot ist in unterer Grafik dargestellt.
r=0,3 Wachstiumsrate
X[0]=1.000.000€ Startwert
K=1.000.000.000 Kapazitätsgrenze

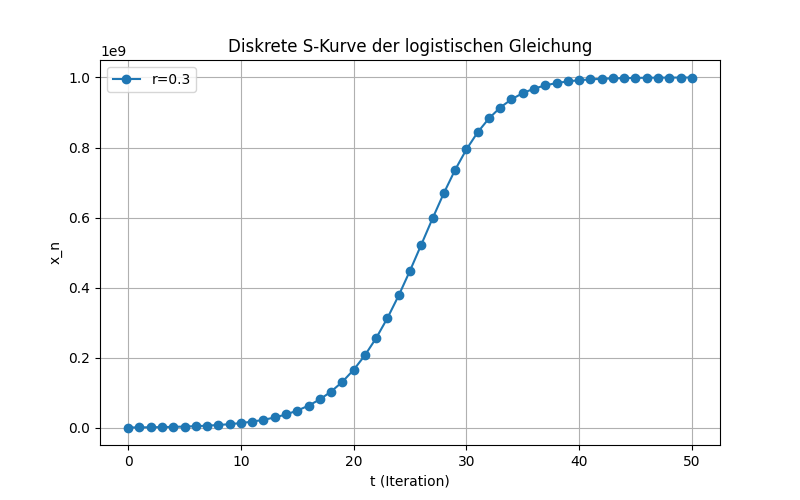
Am Anfang gibt es exponentiells Wachstum. Dann kommt der Wendepunkt 1.000.000.000 / 2. Bei 1.000.000.000 ist die Grenze erreicht.