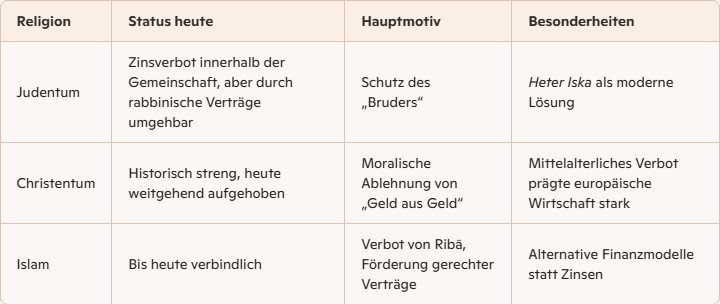
Hier wird als Beispiel die Akkumulation durch ein verzinstes Geld beschrieben. Es gibr aber auch Akkumulation durch Bildung von Kapital.
Geld -> Kapital -> mehr Geld. Oder Wohneigenturm -> Miete -> teuere Wohnungen.
Akkumulation heißt: Kapital vermehrt sich durch die Aneignung von Mehrwert.
Unter kapitalistischen Bedingungen wird der von Arbeiter*innen geschaffene Mehrwert nicht vollständig als Lohn ausgezahlt, sondern vom Kapitalisten einbehalten und wieder investiert, um noch mehr Kapital zu erzeugen. M ist der Mehrwert.
\[
K_{\text{neu}} = K_{\text{alt}} + M
\]
Was bedeutet Akkumulation durch Miete?
Es geht darum, wie Vermieterinnen Kapital anhäufen*, indem sie:
Miete als regelmäßigen Zahlungsstrom erhalten
diesen Überschuss nicht konsumieren, sondern
reinvestieren – meist wieder in Immobilien. Es werden nicht immer Immobilien gebaut, sondern gekauft. Manchmal werden günstige Immoblien abgerissen und durch teuere ersetzt. Wie z. B. Wohnungen der SWSG auf dem Hallschlag
Dadurch entsteht ein selbstverstärkender Kreislauf, der Vermögen konzentriert.
Zur Berechnung des Kapitals nach n Jahren gibt es eine Formel:
\[ K_{\text{ende}} = K \cdot (1+p)^t \ \] \[ \begin{aligned} K_{\text{ende}} &: \text{Endkapital} \\ K &: \text{Anfangskapital} \\ p &: \text{Zins als Dezimalzahl} \\ t &: \text{Zeit in Jahren} \end{aligned} \]Im folgenden ist ein Beispiel für das Endkapital mit dem gleichen Startkapitals und unterschiedlichen Zinsen:

Wenn man die Werte für die Reichen einsetzt: \[ K_{\text{ende}} = 100000 \cdot (1+0.07)^{30} \ \] Man kann den Rechner von Windows verwenden:
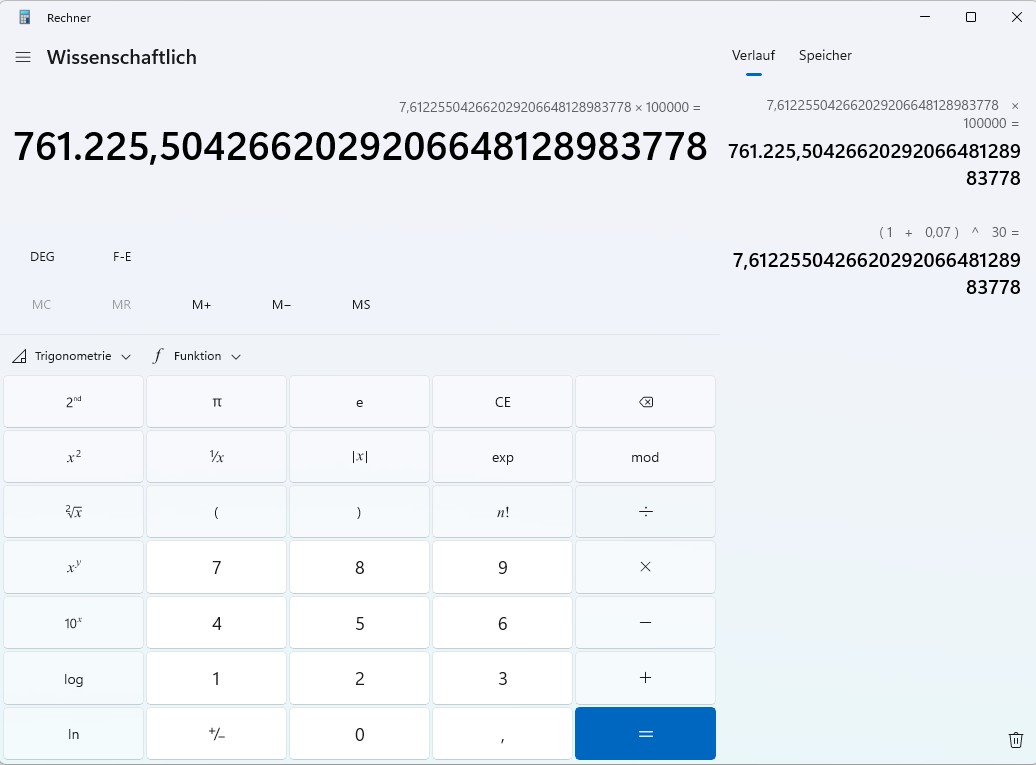
Wenn man die Werte für die Normalen einsetzt: \[ K_{\text{ende}} = 100000 \cdot (1+0.02)^{30} \ \] Man kann den Rechner von Windows verwenden:
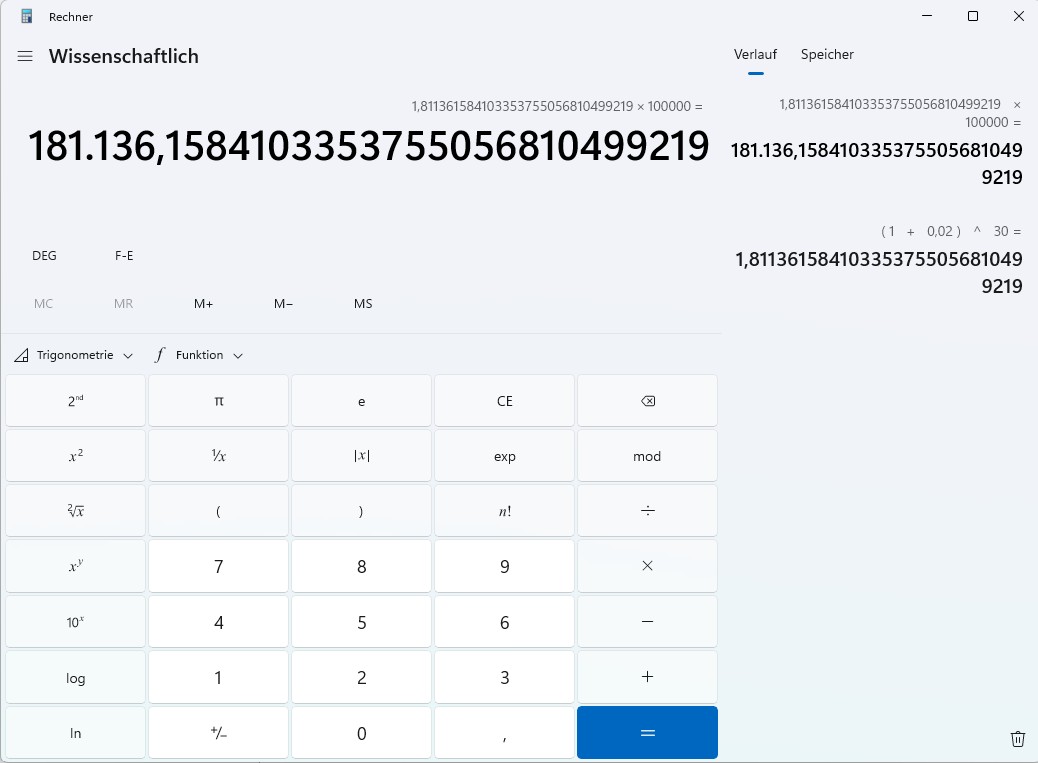
Es gibt verschiedene Variablennamen, wie z. B. K. Diese werden umgeändertt auf x, damit man sie besser vergelichen kann. Für das Kapital gibt es eine geschlossene Formel für den Endbetrag. In anderen Folgen wie z. B. Chaos gibt es keine geschlossesne Folge. Auch werden die jährlichen Zwischenwerte erechnet.
\[ x_{t+1} = (1 + p)\cdot x_{ t } \]Parameter der Folge
\[ \begin{aligned} x_{t+1} = K_{\text{ende}} &: \text{Kapital nach einem Jahr} \\ x_{0} &: \text{Anfangskapital} \\ x_{t} = K &: \text{Kapital zum Zeitpunkt t} \\ p &: \text{Zins als Dezimalzahl} \\ t &: \text{aktuelles Jahr} \end{aligned} \]Es gibt eine Schleife über n = 30 Jahre. Die ersten Jahre sind unten gezeigt:
Man sieht das die Werte ansteigen. In der Systemdynamik und Regelungstechnik nennt man ein solches System instabil. Die Berechnungen kann man mit einem Python Skript machen. Der Plot ist in unterer Grafik dargestellt:
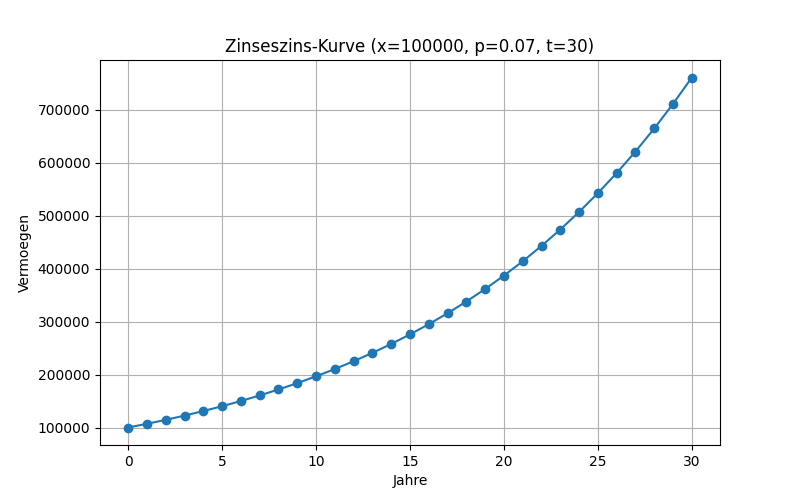
Die Vermögen können nicht unendlich wachsen, weil die Erde beschränkt ist. Ein Beispiel ist der Josephcent
:
Wenn Josef bei Christie Geburt einen Cent angelgt hätte und das Geld verzinst wurde, dann wäre das Vermögen so groß, dass es soviel Wert wäre, wie die Erde aus Gold. Es ist ein Beispiel
für exponentielles Wachstum.
Im Christentum, Judentum und Islam gibt es ein Zinsverbot. Das Zinsverbot im Judentum galt nicht für andersgläubige.